Generierung von Dreieckszahlen

(Sartorius von Waltershausen, 1856)

$D_n$ kann alternativ mit der Gaußschen Summenformel berechnet werden:

$$D_n=\frac{n \cdot (n+1)}{2}$$

Angeblich (Sartorius von Waltershausen, 1856) entstand der Satz, als die Klasse von Carl Friedrich Gauß die Strafarbeit bekam alle natürlichen Zahlen von $1$ bis $100$ aufzuaddieren. Gauß erledigte die Aufgabe in Windeseile. Seine Schnelligkeit ergab sich dadurch, dass er die Zahlen geschickt umgruppierte:

$$1+2+3+\ldots+50+51+\ldots+98+99+100$$

$$=\underbrace{1+100}+\underbrace{2+99}+\underbrace{3+98}+\ldots+\underbrace{50+51}$$

$$=\underbrace{101+101+101+\ldots +101}_{\text{50 mal}}$$

$$=\frac{100}{2}\cdot 101$$

Es zeigt sich also, wie der Name Gaußsche Summenformel bereits verrät, dass der Ausdruck $\frac{n \cdot (n+1)}{2}$ lediglich die Summenformel umschreibt.

Diese kleine Geschichte zu Gauß und die Erklärung zur Formel finden Sie auch in folgendem Unterrichtsvideo.

Durch zwei visuelle Methoden kann diese Überlegung hergeleitet werden.

Überlegung am Rechteck

Bei der ersten Überlegung werden zwei Dreieckszahlen derart nebeneinander gelegt, sodass sich ein Rechteck ergibt. Beispielsweise mit der fünften Dreieckszahl:

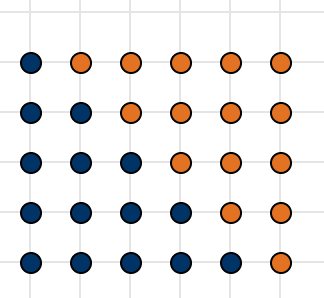
Somit erhält man über die Rechtecksfläche die Gleichung

$$D_5+D_5=5\cdot 6.$$

Wird die Überlegung für allgemeine Dreieckszahlen durchgeführt erhält man

$$2 \cdot D_n= n\cdot (n+1).$$

Durch Umformung ergibt sich:

$$D_n= \frac{n\cdot (n+1)}{2}.$$

Im Unterricht verwendet der Lehrer in Szene 6 dieses Beweisprinzip:

Überlegung am Quadrat

Bei der zweiten Überlegung wird ein Quadrat betrachtet, wobei zwei Dreieckszahlen involviert sind, das orange und das blaue Dreieck. Die Dreiecke werden durch eine grüne Strecke so erweitert, dass ein Quadrat entsteht. Betrachtet wird die Überlegung wieder mit $D_5$.

Die Summe der Kugeln ergibt sich durch:

$$D_5+D_5+6=6^2 \quad \text{ (Länge mal Breite)}$$

Allgemein ausgedrückt:

$$2\cdot D_n+(n+1)=(n+1)^2$$

Durch Umformung ergibt sich erneut:

$$D_n= \frac{n\cdot (n+1)}{2}$$

In beiden Fällen wird also die bereits oben genannte Formel $D_n= \frac{n \cdot (n+1)}{2}$ erhalten, welcher nun auf den Grund gegangen wird.

Beweis durch Induktion

Induktionsanfang Sei $n=1$. Es gilt:

$$\sum_{k=1}^{1}k=\frac{1 \cdot (1+1)}{2}=1$$

Induktionsschritt $n\rightarrow n+1$. Unter der Induktionsvoraussetzung

$$\sum_{k=1}^{n}k=\frac{n \cdot (n+1)}{2}$$

für alle $n\in \mathbb N$ gilt

$$\sum_{k=1}^{n+1}k=n+1+\sum_{k=1}^{n}k \overset{I.V.}{=}n+1+\frac{n \cdot (n+1)}{2}=\frac{(n+1)\cdot(n+2)}{2}.$$

Womit die Gaußsche Summenformel bewiesen wäre.

Abschließend noch einige Beispiele:

Für $n= 2$ ist nach obiger Formel $D_2 =\frac{2(2+1)}{2} =\frac{6}{2} = 3$ oder $D_2=1+2 =3$.

Für $n=3: D_3 =\frac{3(3+1)}{2} =\frac{12}{2} = 6$ oder $D_3=1+2+3 =6$.

$$\vdots$$

Für $n=8: D_8 =\frac{8(8+1)}{2} =\frac{72}{2} = 36$ oder $D_8=1+2+3+4+5+6+7+8 =36$.

$$\vdots$$

Zurück

Weiter