Additionstheoreme

Bei komplexeren Gleichungen und Termen, welche Sinus und Cosinus enthalten, erweisen sich die Additionstheoreme häufig als nützliches Werkzeug. Diese besagen, dass für beliebige $x,y\in\mathbb{R}$ die folgenden Gleichungen gelten:

$$\sin(x\pm y) = \sin(x)\cos(y)\pm\cos(x)\sin(y)$$

$$\cos(x\pm y) = \cos(x)\cos(y)\mp\sin(y)\sin(x)$$

Der Beweis erfolgt durch Einzeichnen der entsprechenden Winkel am Einheitskreis:

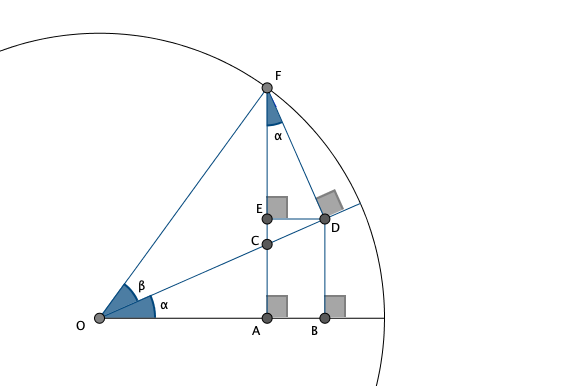
• Zuerst werden die Winkel $\alpha$ und $\beta$ am Ursprung $O$ angetragen.
• Der Punkt $F$, der so auf dem Einheitskreis entsteht, ist somit durch den Winkel $\alpha + \beta$ bestimmt.
• Er wird senkrecht auf die $x$-Achse projeziert, um den Punkt $A$ zu erhalten.
• Der Punkt $C$ ist der Schnittpunkt diese Lotes mit demjenigen Radius, der mit der $x$-Achse den Winkel $\alpha$ einschließt.
• Wird zudem das Lot von $F$ auf diesen Radius gefällt, entsteht der Punkt $D$ als Fußpunkt.
• Wird dieser auf die $x$-Achse projiziert, entsteht $B$.
• Und wird er auf die senkrechte Gerade $AF$ projiziert, entsteht $E$.

Mithilfe dieser Punkte und des Satzes des Pythagoras können nun alle Größen der Gleichung

$$\sin(\alpha+ \beta) = \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta)$$

durch Seitenlängen in diversen rechtwinkligen Dreiecken ausgedrückt werden:

$$\sin(\alpha + \beta) = \frac{\overline{AF}}{1}$$

$$\sin(\alpha) = \frac{\overline{BD}}{\overline{OD}} = \frac{\overline{AE}}{\overline{OD}}$$

$$\cos(\beta) = \frac{\overline{OD}}{1}$$

$$\cos(\alpha) = \frac{\overline{EF}}{\overline{FD}}$$

$$\sin(\beta) = \frac{\overline{FD}}{1}$$

Einsetzen all dieser Größen zeigt die Gültigkeit dieses Additionstheorems. Die anderen drei lassen sich auf ähnliche Weise beweisen.

Alternativ können auch $x\pm y$ in die Reihendarstellung von Sinus beziehungsweise Cosinus eingesetzt, ausmultipliziert und so zusammengefasst werden, dass die rechten Seiten entstehen.

Weiterhin können die Gleichungen oben genutzt werden, um weitere Additionstheoreme und Umformungsregeln herzuleiten. Da diese zahlreich sind, hier nur ein weiteres Beispiel. Für alle $x\in\mathbb{R}$ gilt

$$\sin(2x)=2\sin(x)\cos(x).$$

Weitere Informationen zu den trigonometrischen Funktionen finden sie in (Korntreff, 2017).